
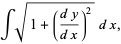
As we see above there are three approaches to represent piecewise functions. Piecewise functions are mainly used to represent functions that have various input ranges with different conditions. Matlab programĬonclusion – Piecewise Function in Matlab This shows that x will take the values from – 5 to + 5. Now, as the ranges are known we need to declare the total range of input variable ‘ x’. In the above example as we know there are two conditions, therefore, we need to define two ranges. Now we will illustrate the above example by using the vectorize approach, First, we need to declare piecewise function like the above examples.Īfter declaring the piecewise function we will define ranges of input variable ‘ x ’. This is the most popular method in piecewise functions. In this method, the input is the whole vector of sequences(conditions) as well as we can combine two conditions by using ‘ & ’ operator. This method is the second approach of piecewise functions without using loops. The above statements represent ranges of x and respective expected function values. Now inside the switch, there will be different cases, our requirement is only cases so we will write 2 cases. The above statement is the keyword for the switch case for changing values of variable ‘ x’. The above statements show f x is piecewise function concerning input variable ‘ x’, after declaring the function we will start with the switch statement. To implement the above example by using the switch – case statement first, we need to declare the function statement ( piecewise function). In this example there are two conditions in function f x, one is less than equal to ‘ 0 ’ and the other one is greater than ‘ 0’.
In this method we represent different conditions in different methods, we can specify multiple cases in one switch loop. The second method in loops is driven by switch-case statements. it shows that if the value of x is less than or equal to ‘ 0 ’ then out will be ‘ – 2 ’ and if the value of ‘ x ’ is more than ‘ 0 ’ then the output will be ‘ 2’. In above statements if-else statement is used to define the range. In the above statement ‘ f x ’ is the name of the output variable, ‘ piecewise ’ is keyword used for the above function and ‘ x ’ is the input variable.Īfter declaring function now we need to define the conditions of ranges of input variable ‘ x’. To implement the above function in Matlab first we need to create one function with keyword ‘ piecewise ’ Plot ( input variable, output variable )įunction output variable = piecewise ( input variable ) This is one of the basic terminologies to implement piecewise functions but, this is not a good practice to implement piecewise function. The vectorized method By using If-Else statements Li, Almost periodic solutions of single population model with hereditary effects, Appl.

Stamov, On almost periodic processes in impulsive competitive systems with delay and impulsive perturbations, Nonlinear Anal. Niu, Periodic solution and almost periodic solution of impulsive Lasota–Wazewska model with multiple time-varying delays, Comput. Stamov, Separated and almost periodic solutions for impulsive differential equations, Note Mat., 20(2000/2001), 105–113. Besicovitch, Almost Periodic Funtions, Dover (New York, 1954). Liu, Almost Periodic Type Functions on Time Scales, Master Degree thesis, Harbin Institute of Technology (2009).Ī. Perestyuk, Impulsive Differential Equations, World Scientific Publishing Co.(River Edge, NJ, 1995).

Zh., 44 (1992), 389–400 (in Russian) translation in Ukrainian Math. Trofimchuk, Spaces of piecewise-continuous almost periodic functions and almost-periodic sets on the line. He, Almost Periodic Differential Equations, Higher Education Press (Beijing, 1992) (in Chinese).Ī. Levitan, Almost Periodic Functions, Gostekhizdat (Moscow, 1953).Ĭ. Zhang, Almost Periodic Type Functions and Ergodicity, Science Press (Beijing), Kluwer Academic Publishers (Dordrecht, 2003).ī. Wexler, The Qualitative Theory of Systems with Impulse (Russian translation), Mir (Moscow, 1971).Ĭ.


 0 kommentar(er)
0 kommentar(er)
